CPSC 370: Functional and Logic Programming (2011)

Homework Questions now Due

Due Friday, October 7, 2011.

Pressman’s instructions) For more details go here.

This question is about sorting and related ideas.

Determine what the order datatype is. Explain how
```
 type α comparator 
  = α * α -> order ; 
```
corresponds to the Java^™ concept of Comparable.
Write a function isSortedwith signature α comparator -> α list -> bool. Test it. (You may wish to note that there are builtin functions Int.compare and String.compare that have the types int comparator and string comparator respectively.)
Write a function insertwith signature α comparator -> α * α list -> α list that inserts an item into a sorted list. Test it.
Write a function insertionSortwith signature α comparator -> α list -> α list that insertion sorts a list. Test it. Re-code this beautifully in one line.

Write a function that counts the number of correct colours in incorrect places (the number of white pegs in the 1970's Mastermind^™ game. See also Pressman’s instructions)

Due Wednesday, November 02.

Given

        datatype α tree 
             = E | T of ( α tree * α * α tree )

write a tail-recursive function that sums the values of an int tree.

Given
```
        datatype choice 
            = Rock | Paper | Scissors 
            | Spock | Lizard ;
        datatype result = win | lose ;
      
```
write something like a partial function from choice * choice to result that plays “rock paper scissors Spock lizard” correctly.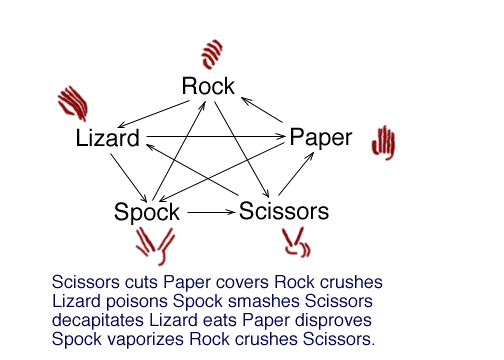
Maximum points for cutely coded solutions.

Due Monday, November 07.

Unicode unifies most of world’s characters by giving each character a code between 0 and 2097151 (2²¹-1), the first 128 of which are identical to ASCII.
UTF-8 is a way to convert a series of Unicode codes to bytes. There is a nice FAQ describing UTF-8 and Unicode.
1. Write a function to convert a list of Unicode values into a corresponding UTF-8 values.
2. Combine the above with CharVector.fromList and Char.chr to get a function that converts an int list of Unicode codes to a CharVector.vector (aka a string).
3. Use the TextIO.openOut, TextIO.output, and TextIO.closeOut functions to write appropriate test strings to a text file. Try displaying the resulting file on a UNIX machine.
Scheme Homework.
Using the relations

write a Scheme program to calculate e to the x. Compare your results with the builtin exp function.

Note that .
Look up the definition of the flatten function, and write and test your own definition.
Look up the definitions of the special forms (and …) and (or …). Explain why these are syntactic sugar for other Scheme forms.

Due.

Determine what the combinator S(S(KS)(S(KK)S))(KK) does.
Hint: The easiest way to unravel this is to un-apply η-reduction. That is, replace
S(S(KS)(S(KK)S))(KK) with
λ f.S(S(KS)(S(KK)S))(KK)(f), apply the combinator rules that you can. Then apply this trick again a couple of times to the body of the simplified
λ f.S(S(KS)(S(KK)S))(KK)(f) expression.

If you have done things correctly, you should end up with short λ-expression of three variables.
Write a Prolog predicate constant/1 that unifies with mathematically constant expressions, that is: numbers; sums, products, and so on, of constants; special constants like pi and e; and functions applied to constants. (You may wish to look at the functor/3 and arg/3 builtin predicates.)
Write a prolog predicate deriv/3 with argument pattern deriv(+Term,+MathVar,-Result) that applies standard first-year calculus derivation rules. The predicate should support application of the chain rule.


	Fall 2011
	2024-12

CPSC 100 [Other years]

CPSC 370 [Other years]

Homework

David’s Schedule